Na Visão Computacional trabalhamos com diversas técnicas para processamento, identificação de padrões e extração dos mais diversos tipos de informações de imagens, porém, muitas vezes, acabamos desconsiderando a importância do instrumento fundamental para o nosso trabalho: A Câmera.
Nesta série de artigos quero trazer os principais aspectos das câmeras para que possamos entender melhor seu funcionamento e sejamos capazes de extrair o máximo de informação que elas podem nos oferecer. Os assuntos abordados serão:
- Fundamentos da Câmera
- O modelo Pinhole
- As partes da Câmera
- Sensores (CCD e CMOS)
Ao final da leitura destes artigos, você terá um melhor entendimento do que são, como funcionam e como você pode utilizar as câmeras da melhor forma possível em seus projetos.
Vamos ao que importa!
A Câmera Escura
As câmeras são construídas aplicando-se conceitos e modelos fundamentais explorados há muito tempo por diversos pesquisadores. Para entender o funcionamento básico das câmeras, precisamos falar sobre A Câmera Escura.
A Câmera Escura foi um experimento realizado utilizando um paralelepípedo oco com paredes internas totalmente pretas, exceto pela parede oposta a um pequeno furo (A) por onde passam os raios de luz e estes projetam-se na parede que não é escura. A Figura 1 ilustra este experimento.
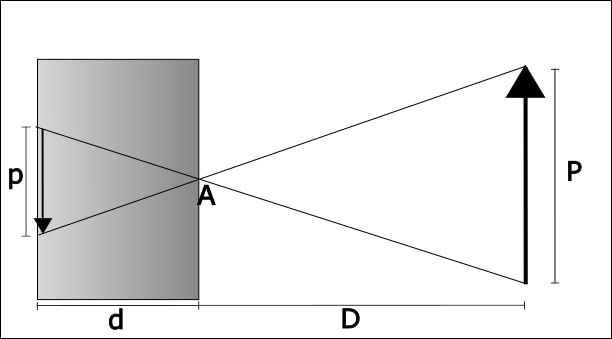
Figura 1: Camera Escura
Fonte: Adaptado de Andrade (2003)
Na Figura 1 temos a representação de um paralelepípedo com uma pequena abertura A por onde os raios de luz (representados pelas finas linhas pretas que se cruzam em A) refletidos por um objeto (a seta), entram e incidem sobre a parede oposta a A, formando uma imagem invertida do objeto em questão. Esta imagem pode ser observada dentro da camera escura quando a parede do fundo é branca ou translúcida.
Da Figura 1 podemos perceber alguns relacionamentos matemáticos que podem nos ajudar a entender como os objetos imageados no mundo real se relacionam com suas representações em uma imagem.
Podemos definir que a escala de representação do objeto (a seta) é:
\[E = \frac{p}{P}\]Se você já tem algum conhecimento sobre as câmeras, já deve imaginar a quem d e D são equivalentes em uma câmera fotográfica. Mas se ainda não faz ideia, não se preocupe, continuaremos a explorar as câmeras e suas propriedades.
Agora que entendemos o modelo mais fundamental de câmera, podemos começar a aproximá-lo das câmeras fotográficas que conhecemos.
Poderíamos inicialmente substituir a parede oposta ao orifício A por um filme fotográfico (coisa antiga, né?), que receberia os feixes de luz que passam por A e registrariam uma imagem. Porém, ainda existe um problema: A imagem projetada seria fraca, pois recebemos uma pequena quantidade de luz, fazendo com que seja necessário um longo tempo de captura para criar esta imagem.
Como podemos resolver este problema? Existe uma forma de registrar esta imagem mais rápido? A resposta é sim! Para isso usamos as lentes! No nosso caso aqui, utilizamos lentes convergentes, pois estas recebem os raios de luz e fazem com que estes convergem para um ponto. A Figura 2 ilustra a Câmera Escura agora com uma lente inserida na abertura A.
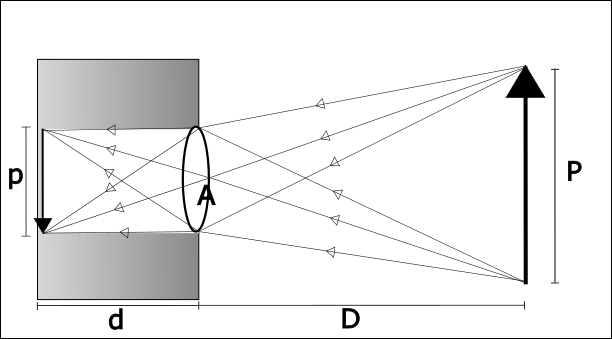
Figura 2: Câmera Fotográfica
Fonte: Adaptado de Andrade (2003)
Agora, com a inserção da lente convergente na abertura A, podemos concentrar um número maior de feixes luminosos na parede do fundo da nossa câmera escura, tornando a imagem construída muito mais luminosa. A propósito, vamos chamar esta parede de plano focal, que é basicamente onde os raios luminosos incidem para formar a imagem do objeto em questão.
Agora você pode estar se questionando: O que acontece se variarmos a distância d mantendo a mesma lente? Se d aumenta,nossa imagem fica maior (alteração de escala), os feixes de luz estarão muito mais espalhados, fazendo com que nossa imagem fique novamente fraca, pouco luminosa, exigindo que deixássemos o nosso filme fotográfico muito mais tempo exposto à luz. Já podemos perceber que d tem uma relação muito importante tanto com a escala de representação dos objetos na imagem, quanto com o tempo de exposição do filme à luz.
A Lei de Gauss para Lentes
Vimos que a adoção de uma lente convergente nos traz benefícios e que existe um relacionamento entre d, o tempo de exposição e o quão brilhosa nossa imagem será se variamos estes parâmetros.
Agora, como saber qual d me dá a melhor imagem possível? Para isso utilizando a Lei de Gauss para lentes, que é definida como:
\[\frac{1}{f} = \frac{1}{D} + \frac{1}{d}\]Note que a fórmula acima contém os seguintes parâmetros:
- f que é a distância focal de uma lente, também conhecida comprimento focal;
- d que é a distância entre o centro óptico da lente e a parede de fundo da câmera escura;
- D que é a distância entre o objeto imageado e o centro óptico da lente.
Vamos agora imaginar que a distância D é muito maior que d. Isto faz com que 1/D tenha um valor muito pequeno, sendo possível desprezar este termo, fazendo com que a equação se torne:
\[\frac{1}{f} = \frac{1}{d}\]Logo, vemos que, quando o objeto está muito distânte da câmera em comparação com a distância entre a lente e o plano de projeção, d é igual a distância focal. Lembra que anteriormente falamos que se você ainda não tinha entendido a quem d e D são equivalentes, nós iríamos esclarecer? Pois é, por este motivo, neste caso, d é igual a distância focal.
Conclusão
Neste artigo abordamos o modelo mais simples de câmera, entendemos o motivo pelo qual usamos as lentes e também conhecemos alguns dos principais parâmetros que relacionam um objeto imageado com sua projeção em uma imagem. No próximo artigo exploraremos ainda mais este relacionamento através do Modelo Pinhole. Nos vemos lá!
Com muito carinho e um pouco de agressão…
Engenheira em Visão Computacional e fundadora do Grupo OpenCVismo Brasil.
Referências
Andrade, J. B., 2003. Bittencourt de Andrade. Fotogrametria. Curitiba.
Thomas A. Stoffregen tas@umn.edu (2013) On the Physical Origins of Inverted Optic Images, Ecological Psychology, 25:4, 369-382, DOI: 10.1080/10407413.2013.839896
https://blog.scienceandmediamuseum.org.uk/introduction-camera-obscura/