Detecção de Bordas
A visão computacional é uma área da ciência que desenvolve teorias e tecnologias como objetivos de extrair informações de dados multidimensionais. Quase sempre, recorremos a uma analogia de como nós detectamos e reconhecemos objetos. Um objeto é caracterizado por conjuntos de atributos como: cor, texturas e forma geométrica. Nesse sentido, a extração de contorno poder representar informações importantes sobre um determinado objeto. Por exemplo, podemos identificar diversas formas geométricas como retângulo circulo, triângulos, linhas e outros. Além do que os médoto de detecção não utilizam muito recurso computacional sendo uma técnica atraente para aplicação em sistemas embaracados.
Nessa capítulo vamos conhecer a base dos algoritmos de detecção de borda e aplicar o algoritmo de Canny.
Dependências
Para executar os scripts mostrado aqui, você precisará ter em sua máquina uma versão do python 3 e o OpenCV instalados.
- python3
- OpenCV
O que é uma borda?
Uma borda á caracteriza por uma variação abrupta entre os pixels vizinhos de uma imagem.
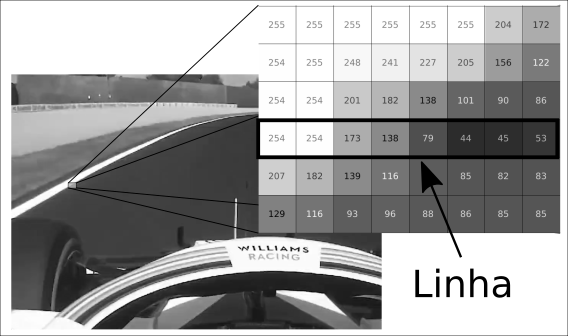
Figura 1: Pista de corrida
Primeiro vamos analizar apenas na linha selecionada Figura 1, podemos representa-la por uma função I(x) cujo domínio é uma lista [254,254,173,138,79,44,45,53]
Como nossa função é discreta (só admite valor inteiro) não podemos calcular diretamente a derivada dessa função mais podemos fazer uma boa aproximação.
A derivada é uma operação matemática que permite calcular a taxa de variação de uma função ou de dois pontos muito próximos. Ela é definida pela equação 1.
Equção 1: Derivada.
Supondo que x seja a posição que estamos na lista, então f(x) é o valor do pixel e f(x+h) é próximo pixel. Acontece que, quando o intervalo h for muito pequeno vamos pegar variações decorreste de ruídos na imagem. sendo assim, não vamos preocupar em fazer pequenos ajustes nesse sentido. Por exemplo, podemo dizer que nossa derivada no ponto x é dada por f(x+h)-f(x-h), ou seja, a diferença do próximo pixel pelo pixel anterior ao ponto x.
Equação 2: Derivada aproximada.
Desconsideramos a divisão por h da Equação 1, porque nesse contexto ele é apenas um normalizador da função, ou seja, ele será um parâmetro que vamos passar ao realizar os cálculos.
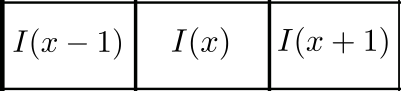
<Figura 2: Derivada aproximada para 1.
Um dos motivos da aproximação de fizemos é por conta dos ruídos, porém essa nova equação pode ser representada por um kernel. Computacionalmente é mais interessante convolver um kernel por uma imagem do que aplicar uma função.
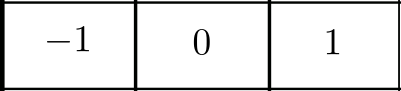
Figura 3: Kernel para calculo de derivada.
Na Figua 4 realizamos essa operação para toda a linha da imagem 1, tente identificar onde está a região que selecionamos.
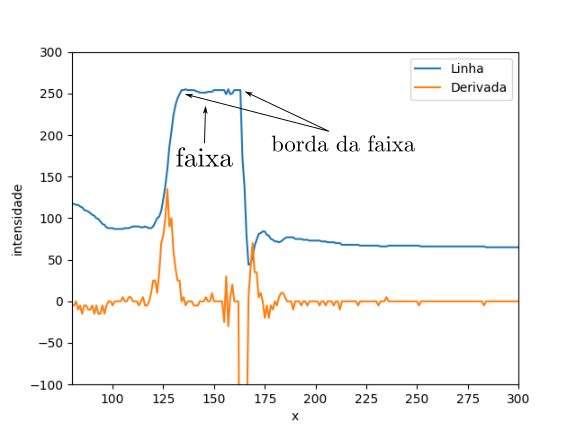
Figura 4: Grafico de linha da selecionada na figura 1.
A lista começa com valor alto, 254 decai ate 44 e sobe novamente para 53. Essa variação acontece no intervalo 160 à 178 (aproximado) do eixo x.
Se expandirmos esse ideia para um plano 2D nossa função anterior pode ser descrita da seguinte forma.

Figura 5: Aproximação de derivada.
Agora temos derivadas parciais. Da mesma forma, podemos rescrever isso por um kernel.
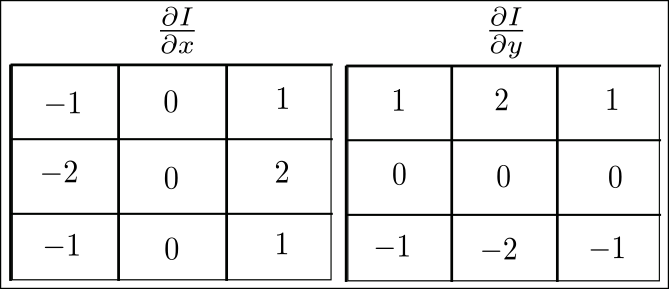
Figura 6: Kernel para derivada parcial.
Esse par de kernel na Figura 6 tem o nome de operador Sobel. O OpenCV tem esse operador implementado aqui cv2.sobel, então vamos usar.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import cv2
ddepth = cv2.CV_16S
# Carrega imagen "frame.png" em escala de cinza
gray = cv2.imread("frame.png",cv2.IMREAD_GRAYSCALE)
# calcula derivada de primeira ordem na direção x
grad_x = cv2.Sobel(gray, ddepth, 1, 0, ksize=3,scale = 1)
# calcula derivada de primieira ordem na direção y
grad_y = cv2.Sobel(gray, ddepth, 0, 1, ksize=3,scale = 1)
# calcula valor absoluto e converte para uint8
abs_grad_x = cv2.convertScaleAbs(grad_x)
abs_grad_y = cv2.convertScaleAbs(grad_y)
# Calcula gradiente
grad = cv2.addWeighted(abs_grad_x, 0.5, abs_grad_y, 0.5, 0)
# concatena image gerada com a original
saida=cv2.hconcat((grad,gray))
# redimenciona em 60%
saida=cv2.resize(saida,None,None,0.4,0.4)
#salva imagem
cv2.imwrite("saida.png",saida)
cv2.imshow("janela", saida)
cv2.waitKey(0)

Figura 7: Resultado do Sobel.
Perceba que aplicamos o operador Sobel duas vezes, primeiro na direção x e depois na direção y. A composição dessas derivadas é matematicamente conhecida como gradiente. O gradiente é um vetor que aponta na direção onde a função tem a maior variação. No entanto, o que nos interessa aqui é magnitude desse gradiente, ou seja, o quão abrupta é essa variação. O módulo do gradiente poder ser calulado usando a Equação 2 (calculamos com a função cv2.addWeighted).
Equação 3: Magnitude do gradiente.
O Sobel é uma das operações mais relevantes para detectar contorno em imagens. Embora exista alternativas como cv2.Scharr que tem uma aproximação melhor da derivada. O Sobel ainda é um dos principais métodos empregados nos algoritmos para detecção de borda.
Algoritmo de Canny
O algoritmo de Canny executa vários estágio para detectar uma borda.
1. remoção de ruídos.
Na Figura 4, o gráfico da derivada apresenta bastante ruido, isso acontece porque pegamos micros variações locais. Canny usa um filtro gaussiano para resolver isso. Veja como o filtro afeta a derivada na Figura 8.
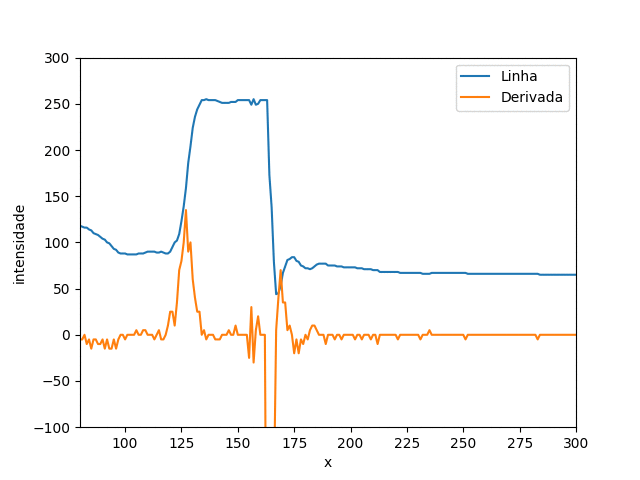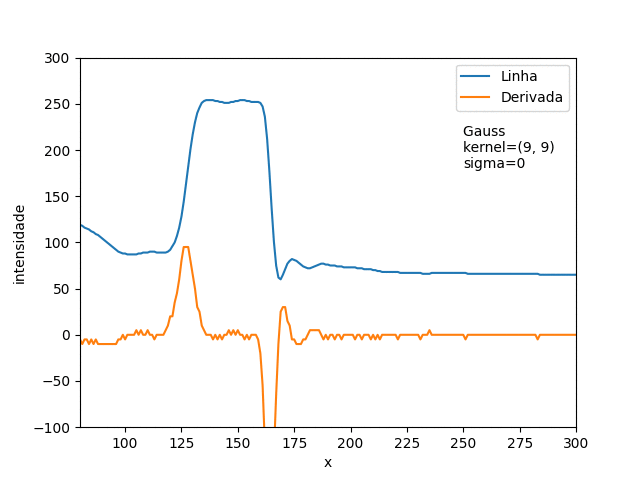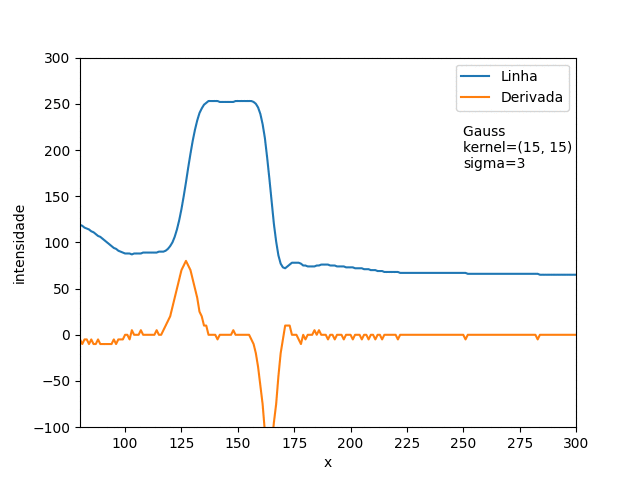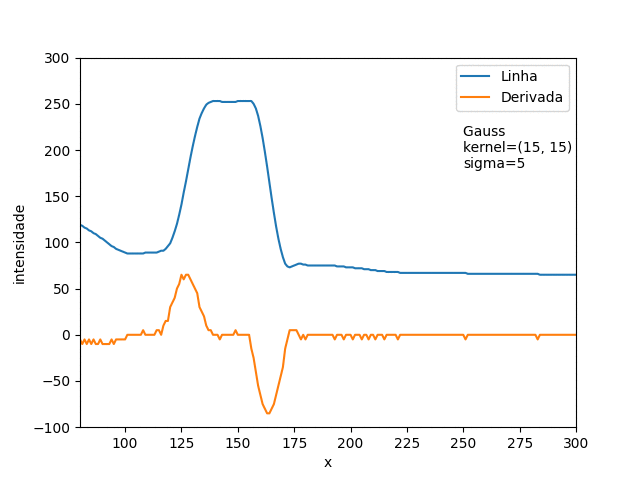
Figura 8: Efeito de filtro gaussiano.
2. Calcular gradientes.
O filtro Sobel discutido no tópico anterior é usado aqui para calcular os gradientes.
3. Máximos locais.
Nessa etapa uma varredura completa é realizada na imagem em busca de gradientes máximos locais, esse processo elemina bordas largas ou duplicadas.
4. Limiar de hesterese.
Tudo que esta abaixo de minVal é descartado. o que esta entre minVal e maxVal é mantido apenas se parte do contorno estiver acima de maxVal. Na Figura 9, A é mantido porque esta acima de maxVal, C é mantido, embora esteja abaixo de maxVal ele esta conectado a A. Já o B é removido, pois esta totalmente dentro da área delimitada.
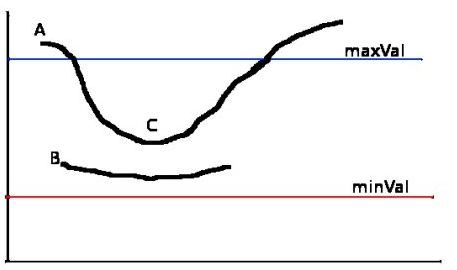
Figura 9: Região delimitada pelos liminar maxVal e minVal.
Fonte:
Usando Canny
No OpenCV temos uma implementação do algoritmo de Canny, o segundo e o terceiro parâmetros passados, são minVal e maxVal.
1
2
3
4
5
6
7
8
9
10
11
12
import cv2
# Carrega imagem em escala de cinza
gray = cv2.imread('frame.png',cv2.IMREAD_GRAYSCALE)
# aplica algoritmo de Canny com minVal=100 e maxVal=200
edges = cv2.Canny(gray,100,200)
# concatena imagem original com o resultado
saida=cv2.hconcat((gray,edges))
#redimenciona
saida=cv2.resize(saida,None,None,0.4,0.4)
#Mostra saida
cv2.imshow("janela",saida)
cv2.waitKey()

Figura 9: Resultado do Canny.
Aqui deixo um vídeo com animação gráfica do que discutimos nesse artigo.
Conclusão
De fato, a área de visão computacional é permeada por aplicações matemáticas de alta complexidade. No entanto, bibliotecas como OpenCV tem simplificado, permitindo que pessoas de diversas áreas desenvolva suas própias aplicações. Se você gostou desse assunto, junte-se a nós no grupo opencvBrasil ![]() .
.
Atenciosamente
Engenheiro eletricista pela UNEMAT e mestrando em Zootecnia na Universidade Federal do Mato Grosso UFMT.
Autor do blog visioncompy
Referências
| Documentação oficial OpenCV v 4.5.0: Sobel. fonte https://docs.opencv.org/master/d2/d2c/tutorial_sobel_derivatives.html |
| Documentação oficial OpenCV v 4.5.0: Algoritmo de Canny. fonte https://docs.opencv.org/master/da/d22/tutorial_py_canny.html |
