Processamento Morfológico de Imagens

Processamento Morfológico de Imagens

Imagens e Conjuntos

Em algumas aplicações de Processamento Digital de Imagens podemos utilizar conceitos da Teoria dos conjuntos para realizarmos algumas análises e inferir certas informações em imagens. Por exemplo, podemos dizer que um objeto, representado em uma imagem, é formado pelo conjunto de pixels que o constituem.

Figura 1: Pista de Corrida

Na Figura 1 você pode perceber facilmente algumas árvores e uma pista de corrida. Podemos dizer que somos capazes de determinar visualmente as diferenças entre as árvores e a pista de corrida apenas afirmando que o conjunto dos pixels azuis formam a pista de corrida, enquanto o conjunto dos pixels de cor verde-escura formam as árvores.

O que eu quero te mostrar neste capítulo é que podemos realizar algumas operações sobre estes conjuntos de pixels que representam objetos nas imagens! A estas operações sobre conjuntos de pixels chamamos de Processamento Morfológico de Imagens.

Os Elementos Estruturantes

Já sabemos que podemos considerar objetos representados em imagens como conjuntos e que podemos também realizar operações sobre estes conjuntos. Bom, mas se vamos fazer operações sobre este conjunto de pixels, precisamos de um outro conjunto para realizar estas operações, não é mesmo? Muito bem! Para realizarmos estas operações precisamos dos Elementos estruturantes!

Observe a Figura 2, na qual temos uma imagem representando um objeto em tons de cinza que é imóvel, enquanto que, se movendo, temos um pequeno conjunto de pixels que está percorrendo esta imagem (algo parecido com um filtro).

Figura 2: Erosão

A Figura 2 mostra uma operação entre dois conjuntos: O elemento estruturante (filtro que se move ao longo da imagem) e o objeto representado na imagem. O resultado desta operação é uma redução da quantidade de pixels que presentam o objeto. Esta operação é chamada de Erosão.

Como funciona a Erosão em uma imagem?

Vamos considerar que o conjunto A é o objeto representado na imagem e que o conjunto B é o elemento estruturante, ambos apresentados na Figura 2.

1. Primeiro é feita uma “varredura” do conjunto B (Elemento estruturante) em A para que a origem de B passe por todos os elementos de A.

2. Depois é feita uma verificação: Para cada localização da origem de B, considera-se que o pixel de A é um membro do novo conjunto caso todos os elementos de B que são diferentes de zero estejam contidos em A, caso contrário, descarta-se este pixel. (No exemplo da imagem, a cor cinza representa o valor 1 e a cor branca representa o valor zero).

3. Depois de fazer essa varedura em toda a imagem, o resultado final é alcançado com o objeto tendo um conjunto menor de pixels conforme mostra a Figura 2.

Outra Operação: A Dilatação

Figura 3: Dilatação

Observe na Figura 3 o procedimento que está sendo representado: Temos o conjunto A (o objeto representado na imagem), o conjunto B (elemento estruturante) e novamente realizamos uma varredura de B em A. A diferença é que agora, ao contrário do processo de Erosão, o objeto representado na imagem não “perdeu” pixels, isto é, ao invés de diminuirmos o conjunto A, ele ficou ainda maior. Quando isto acontece dizemos que o conjunto A sofreu Dilatação.

O que aconteceu neste caso é que modificamos a operação a ser realizada entre estes dois conjuntos para aplicar a Dilatação, assim podemos dizer que a dilatação é aplicada seguindo os seguintes passos:

1. Faz-se uma “varredura” do conjunto B (Elemento estruturante) em A para que a origem de B passe por todos os elementos de A.

2. Depois é feita uma verificação: Para cada localização da origem de B, considera-se que o pixel de A é um membro do novo conjunto se pelo menos um elemento de B esteja contido em A, caso contrário, descarta-se este pixel. Perceba que antes mesmo que a origem do elemento estruturante esteja contida dentro do conjunto A, o pixel abaixo dela já está contida dentro de A, portanto considera-se que a posição da origem do elemento estruturante é parte do novo conjunto A.

3. Depois de fazer essa varedura em toda a imagem, o resultado final é alcançado com o objeto tendo um conjunto maior de pixels conforme mostra a Figura 3.

Mão na massa com a OpenCV e Python

Pré-requisitos

O que será necessário para realizar os tutoriais a seguir:

• Python 3.x instalado em sua máquina;
• OpenCV 4;
• Um editor de código ou IDE de sua preferência (Eu utilizo o VS Code);
• Os dados que utilizaremos para executar os tutoriais podem ser baixados aqui.

Exemplo 1: Erosão

Observe a imagem abaixo. Note que não há muitos detalhes nesta imagem e isso pode facilitar as coisas para nós.

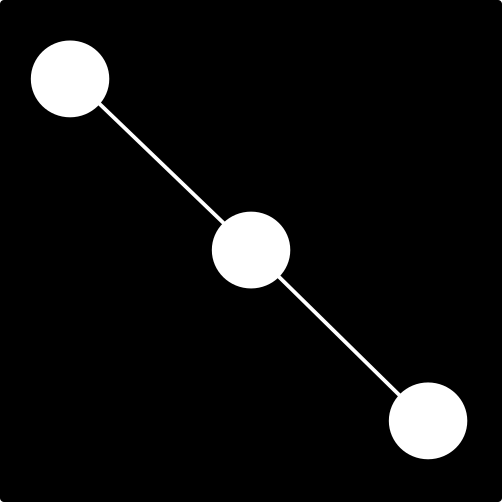
Figura 4: Exemplo 1

Primeiro vamos supor que, por algum motivo, queremos eliminar a linha que conecta os circulos. Esta é uma operação de remoção de alguns pixels, por isso usaremos a Erosão para remover os pixels desta linha.

Com a OpenCV o processo de aplicar a erosão é muito simples:

import cv2, sys
import numpy as np

#lendo a imagem
img = cv2.imread("ex1.png",0)

if img is None:
    print("Não foi possível ler a imagem!")
    sys.exit()

#criando um elemento estruturante de tamanho 5x5
kernel = np.ones((5,5),np.uint8)

#Aplicando a erosão
erosao = cv2.erode(img, kernel, iterations = 1)

cv2.imwrite("erosao_ex1.jpg", erosao)

No código acima utilizamos um elemento estruturante (que também pode ser chamado de kernel) de tamanho 5x5 para aplicar a erosão. Neste kernel, todos os valores são iguais a 1. Você pode criar kernels personalizados que tenham também valores igual a zero, mas aqui utilizamos desta forma para facilitar.

O parâmetro iterations é o número de vezes que a erosão será aplicada à imagem. No nosso caso, aplicamos a erosão apenas uma vez.

E temos o seguinte resultado:

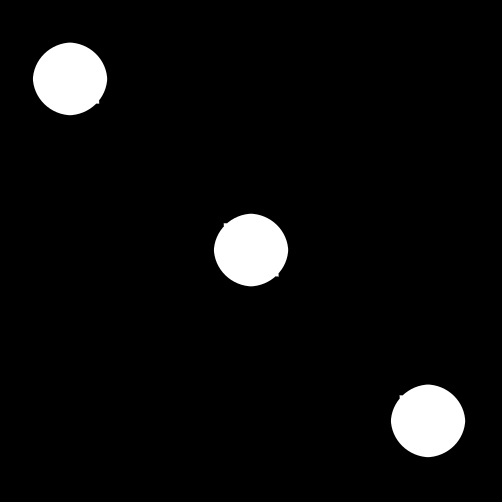
Figura 5: Resultado da Erosão da Fig. 4

Sinta-se à vontade para brincar um pouco com os parâmetros deste trecho de código! Veja o que acontece quando o kernel tem tamanhos menores, tamanhos maiores e quando o número de iterações é maior!

Podemos dizer que as principais aplicações para a erosão são:

• Remoção de ruídos na imagem;

• Remoção de atributos que não são interessantes para a aplicação em questão. Podemos imaginar que os círculos brancos são topos de postes e que a linha era um fio passando por eles. Através da erosão removemos o fio.

Exemplo 2: Dilatação

Vamos supor agora que temos uma imagem na qual os círculos tem alguns “buracos” e queremos fechá-los. Precisamos de uma operação que possa adiiconar pixels aos circulos brancos, logo, precisamos da Dilatação.

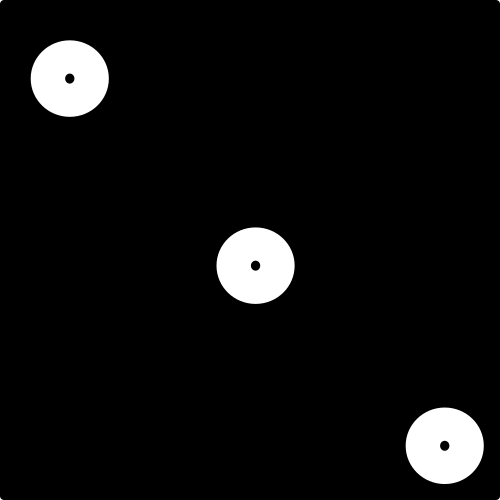
Figura 6: Exemplo 2

E novamente podemos usar a openCV para implementar facilmente esta operação:

import cv2, sys
import numpy as np

img = cv2.imread("ex2.png",0)

if img is None:
    print("Não foi possível ler a imagem!")
    sys.exit()

kernel = np.ones((5,5),np.uint8)
dilatacao = cv2.dilate(img,kernel,iterations = 2)

cv2.imwrite("dilatacao_ex2.jpg", dilatacao)

Neste exemplo usamos o mesmo kernel que utilizamos no exemplo anterior e aplicamos a dilatação duas vezes (iterations = 2) para fechar os círculos brancos.

Temos o seguinte resultado:

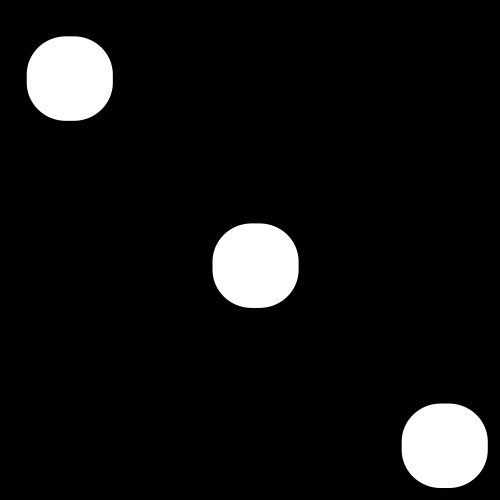
Figura 7: Resultado da Dilatação da Fig. 6

Te convido novamente a realizar testes alterando o tamanho do kernel e a quantidade de iterações para ver o que acontece em cada caso!

Quero novamente chamar a sua atenção para o fato de que nós não apenas “fechamos os círculos”, mas note que os círculos estão maiores do que na imagem original (Fig. 4) e estão assumindo uma forma um pouco retangular, por isso devemos usar a dilatação com cuidado para que não modifiquemos demais as características de um objeto na imagem!

Podemos dizer que as principais aplicações da Dilatação são:

• Quando queremos que objetos sejam “destacados” fazendo com que eles fiquem maiores na imagem;

• Quando queremos “fechar buracos” ou até mesmo conectar elementos que estão muito próximos um do outro na imagem, porém não o suficiente para se conectarem.

---

Atenciosamente
Natália C. de Amorim

Mestre em Ciências Geodésicas e Doutoranda em Ciências Geodésicas na Universidade Federal do Paraná.