Neste artigo falarei sobre o Modelo Pinhonle, um conceito fundamental para entender como relacionamos objetos no mundo real com sua representação no em uma imagem.
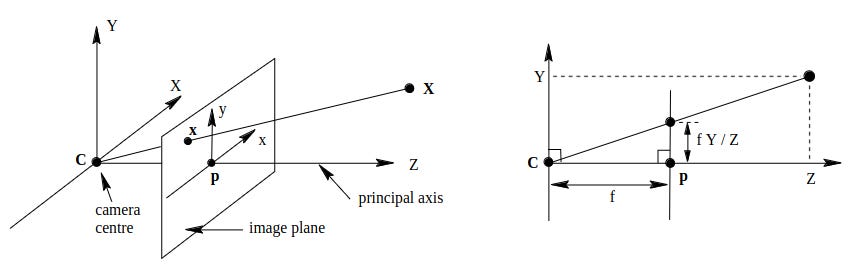
Figura 1: Modelo Pinhole
Fonte: Adaptado de Hartley and Zisserman, p. 154
Na Figura 1, relacionamos um objeto do mundo real (X) à sua representação de plano de imagem (x) usando um sistema de coordenadas (Coordenadas Homogêneas). O ponto C é o Centro de Perspectiva da Lente (PC), e a linha que conecta X, x e C representa um raio de luz, conforme discutido no artigo anterior da Camera Obscura.
A Figura 1 mostra ainda um sistema de coordenadas mundial (X, Y, Z) com sua origem posicionada no centro de perspectiva da câmera (PC). O plano da imagem tem seu próprio sistema de coordenadas com o ponto principal (PP) como a origem (representado na imagem por p). Um ponto de um objeto X no mundo corresponde ao ponto x no plano da imagem. A distância focal (f) é mostrada no lado direito.
Conhecendo todos os elementos representados na Figura 1, podemos agora começar a matemática. Primeiramente, por semelhança de triângulos, podemos afirmar:
\[\frac{y}{f} = \frac{Y}{Z}, \quad \frac{x}{f} = \frac{X}{Z}\]Se isolarmos y, teremos:
\[y = f \frac{Y}{Z} , \quad x = f \frac{X}{Z}\]Este é o modelo pinhole com condições simplificadas (lembre-se de que nossa câmera está posicionada na origem do nosso sistema de coordenadas mundial).
Conhecendo as coordenadas mundiais de um objeto (X, Y, Z), podemos calcular suas coordenadas no plano de imagem (x, y) usando as equações. Por outro lado, com (x, y) e um valor Z conhecido, podemos calcular (X, Y).
Ainda podemos representar estas equações na forma matricial:
\[\begin{bmatrix} x\\ y\\ \end{bmatrix} = \begin{bmatrix} \frac{f}{Z} & 0 & 0 \\ 0 & \frac{f}{Z} & 0 \\ 0 & 0 & 0 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix}\]Relacionar um ponto do plano da imagem (x, y) à sua posição no mundo real (X, Y, Z) requer tanto a distância focal (f) quanto a profundidade do objeto (Z). Em nosso caso simplificado, Z é simplesmente a distância entre o CP da câmera (na origem do mundo) e o objeto.
Agora podemos reescrever esta equação usando um sistema de coordenadas homogêneo para representar nossas coordenadas. Assim, a equação se torna:
\[\begin{bmatrix} x\\ y\\ 1\\ \end{bmatrix} = \begin{bmatrix} f& 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 &1 & 0 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\]Mas o que acontece se a camera não estiver posicionada na origem do sistema de coordenadas mundial?
Para relacionar objetos no mundo real à sua representação no plano da imagem, precisamos saber a posição da câmera (no sistema de coordenadas mundial). Essa posição é definida por dois componentes:
Translação: Um vetor 3D (T) que representa a distância da câmera até a origem do sistema de coordenadas mundial;
Rotação: Uma matriz de rotação 3D (R) especificando a orientação da câmera no espaço. Esta matriz é composta pelos senos e cossenos dos angulos de rotação entre a camera e o sistema de coordenadas mundiais.
Então, podemos aplicar a rotação e a translação às coordenadas do ponto X no mundo e obtemos:
\[\begin{bmatrix} x\\ y\\ \end{bmatrix} = \begin{bmatrix} r_{11} & r_{12} & r_{13}\\ r_{21} & r_{22} & r_{23}\\ r_{31} & r_{32} & r_{33} \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ \end{bmatrix} + \begin{bmatrix} T_x \\ T_y \\ T_z \\ \end{bmatrix}\]Combinando a equação anterior com a última da seção anterior usando a forma de matriz estendida e usando coordenadas homogêneas, obtemos:
\[\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} = \begin{bmatrix} f& 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 &1 & 0 \end{bmatrix} \begin{bmatrix} r_{11} & r_{12} & r_{13} & | & T_x\\ r_{21} & r_{22} & r_{23} & | & T_y\\ r_{31} & r_{32} & r_{33} & | & T_z \\ 0 & 0 & 0 & | & 1 \end{bmatrix} \begin{bmatrix} X \\ Y \\ Z \\ 1 \end{bmatrix}\]Este é o modelo pinhole se desconsiderarmos as distorções na imagem. Em Visão Computacional, a primeira matriz (a matriz que contém a distância focal) é conhecida como matriz de calibração (K).
Conclusão
Ainda não exploramos todas as propriedades do modelo pinhole, mas acho que podemos incluir as distorções da imagem equações em um próximo artigo. Por enquanto, exploramos o modelo pinhole e aprendemos como podemos relacionar as coordenadas de uma representação de objeto em uma imagem com suas coordenadas do mundo real. Vejo vocês no próximo artigo!
Referencias
Multiple View Geometry in Computer Vision, 2nd edition, Richard Hartley and Andrew Zisserman.
Avaliação do desempenho da Técnica Structure from Motion para mapeamento de corredores. Natalia C Amorim