Neste artigo quero trazer uma explicação objetiva do FoV e também mostrar como você pode facilmente utilizar este parâmetro para tarefas como especificação e posicionamento de cameras.
O que é o FoV?
Se tratando de câmeras, o FoV é definido como a área visível que pode ser imageada por um sensor. Em outras palavras, o FoV descreve, de certa forma, o quanto o sensor consegue alcançar dadas as configurações da nossa câmera.
Mas para conseguirmos calcular este parâmetro, devemos entender geometricamente a sua relação com os demais parâmetros de uma câmera. A Figura 1 mostra de forma bem simplificada uma camera com seu sensor, o sistema de lentes (lens), bem como o Field Dimension (que podemos aqui considerar como uma representação do FoV). Esta representação é conhecida como “The thin lens model”.
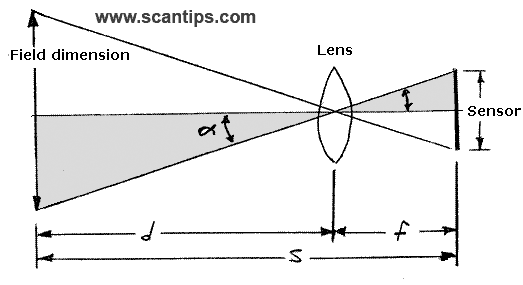
Figura 1: Thin Lens model
Fonte: https://www.scantips.com/lights/fieldofviewmath.html
Antes de cairmos de cabeça na matemática, devemos ter em mente que o FoV pode ser representado através de uma medida angular, ou mesmo medidas lineares como horizontal, vertical ou diagonal. O que determina qual destas formas de representar o FoV é a melhor, são as necessidades do seu projeto.
Na Figura 1 temos, do lado direito em relação às lentes, o plano do sensor e a distância deste plano até o centro óptico das lentes, a distância focal, representada como f. Ao lado esquerdo das lentes temos a plano “observável” pelo sensor e a distância entre o centro optico das lentes até este plano é d. A soma de d e f é S. Além das grandezas já citadas, temos um ângulo alfa que é formado pela linha que parte do centro optico das lentes e é ortogonal aos planos do sensor e o plano da área observável. Este ângulo é muito importante para calcularmos o FoV.
Utilizando trigonometria podemos dizer que:
\[tan(\alpha) = \frac{\frac{sensorSize}{2}}{f}\]Multiplicando a primeira fração pelo inverso da segunda, temos:
\[tan(\alpha) = (\frac{sensorSize}{2f})\]Agora podemos isolar \(\alpha\):
\[\alpha =tan^{-1} (\frac{sensorSize}{2f})\]Porém, observando a Figura 1, percebemos que:
\[FoV = 2\alpha\] \[FoV_{angular} = 2 tan^{-1}(\frac{sensorSize}{2f})\]Assim acabamos de deduzir a fórmula matemática para calcularmos o Field of View de uma câmera. Utilizando valores de sensorSize e distância focal na mesma unidade de medida, você obtém o valor angular do FoV em radianos. Depois basta converter para graus (se for necessário).
Vale ressaltar que na literatura, muitas vezes, podemos encontrar o nome AoV (Angle of View) que detona justamente o que chamei aqui de FoV Angular.
Como calcular o FoV de uma câmera?
Agora que sabemos o que é o FoV e como calculá-lo, é hora de trazermos um exemplo prático para fixar o entendimento deste assunto.
Das equações apresentadas, vimos que, para calcular o FoV, temos que conhecer com uma certa confiança dois parâmetros: A distância focal da lente e o tamanho físico do sensor. Perceba que estou falando do tamanho físico do sensor pelo fato de saber sua resolução não ser suficiente. Por exemplo, saber que um sensor tem 1920 x 1080 pixels não nos dá a informação que precisamos, que é saber suas dimensões físicas, por exemplo, um sensor de 1920 x 1080 pixels, em que cada pixel mede 2,1 x 2,1 micrômetros tem 4,032 mm x 2,269 mm (esta última medida é o tamanho físico do sensor).
Então vamos imaginar uma situação onde eu tenho uma câmera que possui um sensor como o descrito acima e distância focal de 4 mm. Qual o FoV da minha câmera?
De posse da fórmula que deduzimos, podemos calcular o FoV horizontal e o FoV vertical. Então fazemos:
\[FoV Horizontal= 2 tan^{-1}(\frac{4,032 mm}{2 * 4 mm})\] \[FoV Horizontal = 2 tan^{-1}(0,504)\] \[FoV Horizontal = 0,933684972 rad =53,50°\]Agora aplicamos a mesma fórmula para o FoV vertical, usando a dimensão vertical do sensor:
\[FoV Vertical = 2 tan^{-1}(\frac{2,269 mm}{2 * 4 mm})\] \[FoV Vertical = 2 tan^{-1}(0,283625)\] \[FoV Vertical = 0,552733982 rad = 31,67°\]Ok, mas como posso saber as dimensões do FoV?
Se você é como eu, provavelmente saber o FoV em medida angular não é suficiente. Queremos mesmo é saber quantos centímetros vamos conseguir imagear com nossa câmera, não é mesmo?
Pois bem, podemos calcular o FoV em medidas lineares usando fórmulas deduzidas ainda da Figura 1. Primeiramente, vamos relembrar que o angulo alfa aparece tanto no lado esquerdo, quanto direito das lentes (são ângulos opostos e possuem o mesmo valor), assim podemos dizer que, para o lado direito das lentes:
\[tan(\alpha) = \frac{\frac{sensorSize}{2}}{f}\]e para o lado esquerdo, temos que:
\[tan(\alpha) = \frac{\frac{FoV}{2}}{d}\]Como conhecemos o valor de alfa e o valor de d, podemos calcular nosso FoV linear manipulando a equação acima:
\[tan(\alpha) = \frac{FoV}{2d}\] \[tan(\alpha) 2d = FoV\] \[FoV = 2 tan(\alpha) d\]Então, usando os dados do exercício anterior, vamos supor que colocaremos nossa câmera a 1 metro de uma superfície a ser imageada. Podemos calcular os valores do FoV horizontal e vertical como:
(Lembrando que dividimos o valor do FoV Angular por 2, pelo fato de que alfa equivale a metade do FoV angular)
\[FoV Horizontal = 2 tan(\frac{0,933684972}{2}) * 1 metro\] \[FoV Horizontal = 1,008 m\] \[FoV Vertical = 2 tan({0,55273398}{2}) * 1 metro\] \[FoV Vertical = 0,56725 m\]Em resumo
Se você veio aqui só pegar as fórmulas e vazar, tá na mão:
\[FoV_{angular} = 2 tan^{-1}(\frac{sensorSize}{2f})\] \[FoV = 2 tan(\frac{FOV_{angular}}{2}) d\]Se você calcular com o tamanho horizontal do sensor, obtem o FoV horizontal. Se calcular inserindo o tamanho vertical do sensor, obtém o FoV vertical.
Conclusão
Desta forma ficou bem tranquilo entender e calcular o FoV, não é mesmo? Pensando em facilitar a vida para projetos futuros, criei uma planilha onde você pode calcular o FoV inserindo informações de uma câmera (distância focal e tamanho do sensor) e a distância entre a câmera e o plano a ser imageado. Bem prático e você pode usar sempre que necessário!
Acesse a planilha em: aqui!
Com muito carinho e um pouco de agressão…
Engenheira em Visão Computacional e fundadora do Grupo OpenCVismo Brasil.
Referências
https://www.edmundoptics.com/knowledge-center/application-notes/imaging/understanding-focal-length-and-field-of-view/
https://www.scantips.com/lights/fieldofviewmath.html
https://www.scantips.com/lights/fieldofview.html